I N my ,previous article, published in last week's issue of
Page 22
Page 23

If you've noticed an error in this article please click here to report it so we can fix it.
" ,The 'Commercial Motor," in which I drew attention to the fact that common bricks differ in weight to as great an extent as 2+ tons per 1,000 in the Home Counties, to as much as 4 tons per 1,000 in the northern counties. I proceeded to dealwith the problem of assessing rates for brick haulage in the Midlands, This was the outcome of an inquiry from a Midlands operator who told me that bricks in that district weighed 2+ to 2+ tons per 1,000.
This inquirer was interested in the conveyance of bricks in lorries capable of carrying 5-6 tons, so I assumed, therefore, as a basis -for calculation, that he would carry 2,000 per load. On that assumption I drew up a schedule of rates rising from the minimum of Os. 2d. for a one-mile lead, to 33s'. 4d. for a 30-mile lead, for bricks that are tipped at the destination point. For bricks that had to be stacked the rates are increased by 2s. per 1,000.
I now propose to apply the same method in order to arrive at a schedule of rates for the conveyance of bricks in the Home Counties where• the weight is usually round about 21 tons per 1,000, which means that, on a 5-6-ton lorry, it is possible to carry 2,500 bricks per load. Indeed, that is the standard for hauliers who do not habitually overload their vehicles.
Those who do so, often carry 3,000 such bricks per load but, as that is definitely overloading, in connection with which it is impracticable to. assess a schedule of rates , on any reliable basis, I do not propose to deal with it.
Terminal Charges Not Based on Number of Bricks The basic figures which I shall use are, of course, the same as before. namely 5s. 6d. per hour and 9d. per mile for the operation of the vehicle. The terminal charges will not be in proportion :to the number of bricks because, in the period of 90 minutes which I allowed for a load of 2,000 bricks, there was a not inconsiderable allowance for waiting time which, of course, does not vary in proportion to the number of bricks carried. For this load of 2,500, the terminal period of 1+ hohrs, instead of hours, will suffice.
The time allowance of 11 hours at 5s. 6d. per hour is 9s. 7+cl. That is for the vehicle or 2,500 bricks, so that the terminal charge per 1,000 bricks must be Sc. 10d., calculated to the nearest penny,
• I -proptase again to take 25 m.p.h. as the average speed of the 3elticle, and that means, as I showed•in the previous article, that the cost for only time in travelling the• two miles invOlved per one-mile leacHs 11,28. To that must be added 1s. 6d., the cost of running two miles at 9d. per mile,
giving a total of 1s. 11.28d, for the vehicle which is 9.3d. ' per 1,000 bricks per mile lead.
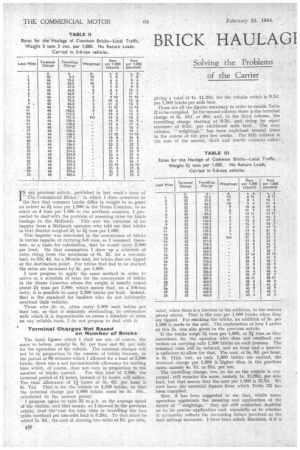
Those are all the figures necessary in order to enable Table II to be compiled. In the second column there is the terminal charge of 3s. 10d: or 46d. and, in the third column, the travelling charge starting at .9.3d. and rising by equal amounts of 9.3d per additional mile lead. The next column, " weightage," has been explained several times in the course of the past -few weeks. The fifth column is the sum of the second, third and fourth columns caku lated, when there is a fraction in the addition, to the nearest penny above. That is the rate per 1,000 bricks when they are tipped. For stacking the bricks, an addition of 2s. per 1,000 is made to the rate. The explanation of how I arrive at this 2s. was also given in the previous article. If the bricks weigh 3i tons per 1,000, or 31 tons as they sometimes do, the operator who 'does not overload can reckon on carrying only 1,500 bricks on each journey. The terminal time will be reduced, and an hour and a quarter is sufficient to allow for that. The cost, at 5s. 6d. per hour, is 6s. 11-id. but, as only 1,500 bricks are carried, the terminal charge per 1,000 is higher than in the previous cases, namely 4s. 7d. or 55d. per ton.
The travelling charge, too, so far as the vehicle is concerned, still remains the same, namely is. 11.28d. per Mile lead, but that means that the cost per 1,000 is 15.5d. We now have the essential figures from which Table III has . been compiled.
Now, it has been suggested to me that, whilst many operators appreciate the meaning and application of the factor 'of " weightage," they are still somewhat doubtful as to its precise application and, especially as to whether it accurately reflects the increasing delays involved as the lead mileage increases. I have been asked, therefore, if it is possible, to make that allowance in a more direct manner so that the reader can judge for himself how far he agrees. and where the conclusions are in line with his own experience. Furthermore, I have been asked to give particulars of how the rate per hour and per mile, for running the vehicle, hat been assessed. I do not propose to. retrace my steps, but will comply with this request in dealing with the haulage of bricks in the larger types of vehicle, in this instance the maximum-load six-wheeler which should carry 12 tons. I will begin, therefore, by setting out the details of current operating costs of a vehicle of this type.
Operating Costs of Maximum-load Six-wheeler .
The standing charges, per 48-hour week, are as follow : Licences, . £2 4s.; wages, including National Health and Unen3ployment Insurances, employers' liability insurance and provision for holidays with pay, £4 16s.; vehicle insurance, £1 10s.; interest on capital outlay, £2 10s.; establishment charges, including the rent of the. garage, £6 • (minimum). The total of these standing charges is £17 per week. To that, add 20 per cent, for net profit, £3 Ss., making a total charge, for only time per week, to be £20 Ss. That is Ss. 6d. per hour.
The running costs per mileof an oil-enginec112-tonner are: Fuel oil, 2.00d. ; lubricants, 0.22d.; tyres, 3.00d.: maintenance, 2.00d.; depreciation, 2.78d. Total, 10d. per mile to which add 20 per cent, for net profit giving us a running charge of is; per mile. That gives me 8s, 6d. per hour, and is, per mile, as the basic figures on which to assess the rates for .brick haulage, using. a vehicle of this type.
The load, carrying bricks in the Horne Counties-1-2i tons per 1,000-will be 5,500 bricks. The terminal period providing for the „loading and tipping of 5,500 bricks, also for waiting time, may be taken to be three hours. That involves the charge for only terminals of £1 5s, Od. for the vehicle, which is quite near enough to 5s. per 1,000 bricks.
Now we come to assessing the time charge for travelling, and it is here that we must make such provision as will allow for slow average speeds over short leads, so that there is no need to make provision for weightage.
For a one-mile lead the average speed is most unlikely to exceed 5 m.p.h., and the time taken to travel the two miles involved in.the one-mile lead is thus 24 minutes. The .cost of 24 minutes, at 8s. 6d. per hour, is 25. 5d. To that must be added the 2s. for the travelling charge at is. per mile, giving us a total of 5s. 5d. for running the vehicle over the journey involved in a one-mile lead: That, as near as .makes no matter, is is. per 1,000 bricks, arid the rahper 1,000, therefore, for a one-mile lead, is Os.
• Average Speed Increases as Lead Mileage Goes Up The second lead mile will be covered at a slightly increased 'speed: 71 m.p.h. is likely to be approximately correct. The time for two miles, at 7i m.p.h., is 16 minutes, which costs 2s. 4d. Adding the 2s. for the running charge, we get 4s. 4d. as the total cost of that second-mile lead. That is the charge for the vehicle carrying 5,500 bricks, and the charge per• 1,000 works out, as near as makes no matter, at 10d. That 10d. is added to the Os. for the first mile, giving us Os. 10d.
• The third mile, when the lead, mileage is increased to three, will be travelled at 10 m.p.h. and the two miles involved will, therefore, take 12 minutes, costing is. 9d. The total cost is 3s. 9d., which is equivalent to 9d, per 1,000 bricks. Adding 9d. to the 6s. 10d. for the two-mile lead, gives us 7s. 7d. as the rate for that distance.
It should be noted, most particularly, having in view what 1-have said in an article, recently, on the liability to make mistakes in applying averages to speeds of travel in assessing a rates schedule, that I have not said that the average speed over the whole three miles is 10 m.p.h. I have only stated that, for the first mile, the average speed can be taken as 5 m.p.h., for the second 7i m.p.h. and for the third 10 m.p.h.
How Rates are Affected by Extent of Lead Mileage ,
Actually, for the three-miles lead, the vehicle has travelled six miles and it has taken a total time of 24 minutes; phis 16 minutes, pins 12 minutes-52 minutes in all; the average speed is thus a fraction short of 7 /m.p.h. For the next seven miles, that is up to a lead mileage Of 10, an'avelage speed of 12 m.p.h. can be taken as likely to be achieved. On that basis the cost of time for running two miles is is. 7d.' the total cost 3s. 7d., which is equivalent to 8d. per 3,000 bricks per mile lead. The rate from three miles
• to 10 miles, therefore, is calculated by adding 8d. for each additional mile lead, and that is what has been done in Table IV.
For the next five miles, that is up to 15-miles lead, the average speed may be taken as 15 m.p.h. and, in the same way as before, it may, be shown that •that involves an addition of 7d. per 1,000 per mile lead.
Beyond the 15-miles lead the maximum legal limit of 20.m.p.h. can be taken to apply, and that means an addition of 6id. per 1,000 per mile lead. In the Table, I have added' first, 7d. and then (Id. and, alternatively, 7d. and 6d. throughout, so as to avoid the use of the id. in the rate. It is interest to note, comparing this schedule with the corresponding one in Table H for bricks of this weight, carried in 5-6-ton vehicles, that there is an economy in employing the larger vehicle, starting at 4d. per 1,000, for t,,hc one-mile-lead and rising to 3s. MI. in the 30-mile lead.




















































