Calculating a Rate for Sam
Page 22

Page 23
Page 25

If you've noticed an error in this article please click here to report it so we can fix it.
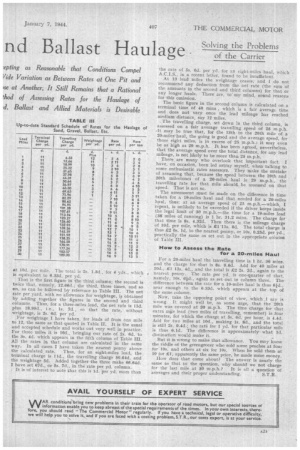
Solving the Problems Solv nd Ballast Haulage of the• Carrier ACCOMPANYING this article is Table II, which is reproduced from my last week's contribution, towards the close of which I had commenced to explain its details. It comprises a schedule of rates, per ,yard' and per ton, for the haulage of sand and gravel as agreed in the Eastern Area of A.R.O. I have already explained how the fighres in the . second and third columns are calculated. " An explanation of the fourth column comes
Ilext. ,
The title of this column is " Short-haul and Weightage per Yd." It provides for the rate to be ," weighted," so that for short hauls' itexce,pds the calculated average, and for longer hauls it is Made less than the calculated rate. The term " weighted " is one commonly used in statistics and implies the correction of " average" figures to corn7 pensate for known factors, the effect of which is to "add to or subtract from the result of a straight calculation.
In, this example, the figures in the second and third columns are the result of a straight calculation, assuming an average time for terminal delays and an average speed of travel from point to point, going from the pit to the destination and returning. .
The known factors which neceesitate the weightage are the diminution in this point-to-point speed over short distances and the extended terminal delay consequent upon the fact that a driver on short hauls is apt to spend a little more time at loading and unloading points, when his travelling time is short. This is natural and only to be expected, because the travelling time is, in one sense, a.' rest: if the rest time be -short the man becomes less energetic in his efforts when loading and unloading. This factor is, of course, of much greater consequence when the sand or gravel is hand loaded and when the tipping gear on the vehicle is hand operated.
Weightage—Its Primary Purpose and Method of Application In other words, weightage is a Method of correcting the theory of calculations in line with the results of practical experience.. It is not, therefore, to be as:sessed by the use of any formula : iL is an addition or subtraction designed to make the rate fit the job as it is carried out. Now, the rate ' for ,a one-mile iead, according to the theoretical figures of the second and third columns, is 10d.
plus 5d., that is 1s. 3d. per •yd. That, as practical experience would dictate, is quite insufficient: is. is, therefore, added, bringing the rate to 2s.3d, which, at the time this schedule was prepared, was fair and reasonable.
The weightage is gradually diminished as shown in Table II, falling by Id. for each addition of one mile to the length of haul until, at a lead mileage of 13, it disappears. After that distance, the compiler proceeds to subtract Id. per mile from the calculated rate, the amount subtracted increasing by hi. for each addition to the lead mileage. There he and I part company, for I am quite sure that, if the basic calculations from which the figures in the second and third columns are derived be correctly made, no weightage of any kind is needed.
. Incidentally-, there is a series of errors in Table II, as the compiler, from 25 miles on, has omitted to subtract the weightage. Whether that omission be deliberate I am not in a position to state. The point is to a certain ceetent immaterial, because I now propose to draw up a schedule of my own, based upon current costs and charges. The figures that I shall use are the up-to-date time and mileage charges for a 5-ton tipper engaged on this class of work. I specify a tipper and the work because the costs and, therefore, the charges, are necessarily above the average. To-day, having in mind the recent increase in wages, and the extra cost of maintenance and tyres, the appropriate figures are 5s. 6d. per hour and 10d. per mile.
Next we must have agreement on two more items— terminal delays and the average speed of travel. AS to The first, 40 minutes—the -time stipulated inTable II-seems reasonable to me. .It should be ncited that it is not suggeSted that a vehicle cannot be .chute—or hopper-e
a20 loaded, and unloaded by tipping, in a total time which is less than 40 minutes: of course it can..
There-is, in the 40 minutes, provision for delays at both ends of the journey—awaiting turn, getting into 'awkward positions for unloading and waiting for the right quality of stuff to become available. These and other obstacles to free loading and unloading are not rare and unusual: they' are customary and they justify an average allowance of 40 minutes,
oncerning the average speed of travel, it is essential to avoid an -error which so many make when dealing with problems of rates for short-haul traffic, especially when compiling a sehedule.such as. this, in which it is intended to introduce the factor of weightage for the ultra-short hauls. If weightaae is to be added to what I might call the lower register of lead distances, then the average speed which must be taken as the basis of the major calculations_ must be that which the vehicle can he expected to maintain over the mediumto long-distanee hauls.
Need for Observing the Maximum Legal Road Speed
One more qualification, that mentioned in the previous article as one . of the conditions attaching to the Air Ministry schedule -of rates for this traffic—the maximum legal road speed must not be exceeded. Assuming that the vehicle, capable of carrying 4 yds., with which, we are concerned weighs less than 3 tons unladen, that is 30 m.p.h. On that basis I am not justified in taking the average speed. to be more than 25 m.p.h. Now we can get on. For the second eblumn, " Terminal Charge per Yd.," _ take the termirm.1 time of .40 minutes ; at 5s. 6d. per hour that is 3s. 8d: That is for 4 yds., so-that the rate per yd. is 11d.
The figure for the third column must be ,arrived at by the use of the charges for time and mileage. In calculating it the fact Mast not be overlooked that for each mile lead the vehiele travels two miles. The time taken, .at 25 m.p.h., is 4.8 mins. and the charge for that, at 5s. 6d. per hour, is 5.3d. To that must be added the charge for two miles
at 10th per mile. The total is 2s. I.3d., for 4 yds., which is equivalent to 6.33d, per yd.
That is the first figure in the third column; the second is twice that, namely, 12.66d.; the third, three times, and so on, as can be followed by reference to Table III. The net rate per yard, with no allowance for weightage, is obtained by adding together the figures in the second and third columns. Thus, for a three-miles lead, the net rate is lid. plus 18.99d., i.e., is. 7d., so that the rate, without weightage, is 2s. 6d. per yd.
• For weightage I have taken, for leads of from one mile to 12, the same as that quoted in Table IL It is the usual and accepted schedule and works out very well in practice:" For three miles it is 10d., bringing our rate of 2s. 6d. to the 3s. 4d. which appears in the fifth column of Table III. All the rates in that column are calculated in the same way. In all cases I have taken the nearest penny above
the calculated rate. Thus, for an. eight-miles lead, the terminal charge is 11th, the travelling charge 50.64d. and the weightage 5d. •Added together the three make 66.64d. I have set 67d., or 5s. 7d., in the rate per yd. column.
It is of interest to note that this is Id. per yd, more than the rate of 5s. 6d. per yd. for an eight-miles haul, which A.C.I.S., in a recent letter, found to be insufficient.
At 13 lead miles the weightage ceases, and I do not 'recommend any deduction from the net rate (the sum of the amounts in the second and third columns) for that or any longer hauls. There are, to' my mind, sound reasons for this omission.
The basic figure in the second column is calculated on a terminal time of 40 mins , which is a fair average time and does not vary once the lead mileage has reached medium distance, say 12 miles.
The travelling charge, set down in the third column, is assessed on a fair average travelling speed of 25 m.p.h. 'It may be true that, for the 13th to the 20th mile of a 20-nailes'haul, the going is good and the average speed, for those eight miles, is in excess of 25 m.p.h.: it may even be as high as 29 m.p.h. It has been agreed, nevertheless, that the average speed over the total distance, for any lead mileage, is not likely to be more than 25 m.p.h.
There are many who overlook that important fact. I have, on occasion, been led astray myself, when talking to some enthusiastic rates assessors. They make the mistake of assuming that, because the speed between the 19th and 20th milestones of a 20-miles haul is 29 m.p.h., the travelling rate for that mile should be assessed on that speed. That is not so.
The assessment must be made on the difference in time taken for a 19-miles haul and that needed for a 20-miles haul, thus: at an average speed of 25 m.p.h.-whieh, I repeat, is unlikely to be exceeded if the driver keeps inside the legal limit of 30 m.p.h.-the time for a 19-miles lead (38 miles of running) is 1 hr. 31.2 mins. The charge for that time is 8s. 4.32d. Then there is the mileage charge of 10d. per mile, which is 21 '11s. 8d. The total charge is thus £2 Os. Id. to the nearest penny, or 10s, 0.25d. per yd., practically the same as set out in the appropriate column of Table III. "
How to Assess the Rate for a 20-miles Haul For a 20-miles haul the travelling time is 1 hr. 36 mins, and the charge for that is 8s. 9.6d. Add for 40 miles at
• 10cl., £1 13s. 4d., and the total is £2 2s. 2d., again to the nearest penny. The rate per yd. is one-quarter of that, namely, 10s. 6d., again as set out in column three. The
• difference between the rate for a 19-miles haul is thus 61d., near enough to the 6.33d. which appears at the top of the same column.
Now, take the opposing point of view, which I say is wrong. It might well be, as some urge, that the 20th mile was covered at 30 m.p.h. The time charge for that extra. Inge lead (two miles of travelling, remember) is four minutes, for which the charge at 55. 6d. per hour, is 4.4d. Add for two miles at 10d., making 18. 8d., and the total is still 2s, 0.4d.; the-rate for I yd. for that particular mile is thus 6.1d. The difference is approximately what Id. diminution would make it.
But it is wrong to make that allowance. You may know the riddle of the greengrocer who sold some peaches at four for'10s. and others at six for 10s. When he sold them at 10 for £1, apparently the same price, he made more money.
How does that come about? The answer is nearly the same as that to the question, why should we not charge for the last mile at 30 m.p.h.? It is all a question of averages and their proper understanding. S.T.R.
The large tank (3) has a capacity up to two tons and is used.to carry liquid carbon-dioxide at a pressure of up to 700 lb. per sq. in. In order to maintain the internal low temperature, which is of the order of zero degrees F., the tank is heavily lagged.
If there be time, or the circumstances are such that the use of a hose is indicated, then this is to hand immediately behind the tank as shown at 4. Instant action can, however, be taken with the aid of the forward nozzle (1), the discharge from which is under control from the driver's cab. This nozzle ejects a mixture of carbon-dioxide in both gaseous and "solid snow" forms and on account of its blanketing action it is; as is well known, a most effective extinguisher.
It will be ncited that there is a second storage tank (2) at the front end of the body. This is for water and has a capacity of 100 gallons. The water, under pressure from the CO, tank, is projected on to the fire through a: suitable length of small-bore hose. There is, of course, a control valve between the CO, tank and the water tank pressure regulation. A refrigerating unit (5) is carried on the vehicle for the purpose of maintaining the necessary low temperature in the storage tank. This unit is driven by a mains electric motor so that it is usable only when the vehicle is resting at its station.
Thg foregoing particulars refer to a new piece of mobile fire-fighting equipment by Cardox (Great Britain), Ltd., 20, Copthall Avenue, London, E.C.2. It is covered by patent No. 556,978, in which there are 24 drawings and a detailed description of the numerous fittings.




















































