LOADS and SPEEDS
Page 31
Page 32

If you've noticed an error in this article please click here to report it so we can fix it.
DETERMINE RATES
IN the previous article figures were [calculated for the cost of operation and for the rate to be charged for time and mileage in relation to six different types of vehicle, assuming that all were engaged upon the cartage of bricks. Details of the costing were given in Table 1, which appeared with that article. From that information, the time and mileage figures, which are set out this week in Table H, were calculated. These figures will be useful in connection with what follows.
The sizes of vehicle, as enumerated, were 5-ton and 6-ton petrol-engined vehicles, and 6-ton, 7-8-ton, 12-ton and 14-ton oilers. Assumptions were made as to the time needed to load and unload. these various vehicles when engaged on brick haulage, and half an hour was allowed in each case for delays not directly connected with loading and unloading. The total terminal times were agreed as set out in Table Ill. From those terminal delay periods the terminal charges, assessed on the basis of rates per hour in Table 11, are also laid down and are included in Table III.
Up to now I have dealt with the first, second and third of the six types of vehicle enumerated, and it is important to note that the maximum legal speed of these vehicles is 30 m.p.h. In that particular they differ from the other three, the speed limit of which is 20 m.p.h. It will be interesting to note how this differentiation in speed affects the cost and the rates to be charged for the haulage of bricks
Calculating Average Speeds
It will be reasonable to assume that the first and last nalf-mile of each journey will be covered by the heavier lorries at the same average speed as the lighter types of vehicle. There is usually plenty of power available in the larger machines and an average speed of 6 m.p.h. for the first and last half-mile of each journey is not excessive, even in the case of the 14-tonner. These two half-miles will be covered in 10 minutes, or a total of 20 minutes for a mile lead.
The second half-mile, it is assumed, will he covered in 21 minutes at an average speed of 12 m.p.h., making a total of 10 minutes for the second mile lead. The total time needed for a two-mile lead will, therefore, be the 20 minutes for the one-mile round trip, plus 10 minutes for the second.
It is assumed that the third half-mile will be covered in I* minutes at an average of 18 m.p.h. Consequently, about 61 minutes is the total time needed for the third mile of any lead. The travelling time necessary for the out and homeward journey of a three-mile lead will thus be 20 minutes for the first mile, 10 minutes for the second, and 61 minutes for the third, a total of 361 minutes for the double journey.
Beyond three miles I am going to assume that the average speed is 20 m.p.h. (3 minutes per mile). After the third mile, therefore, there will be an allowance of 6 minutes per mile lead The above is the basic information from which we can compile actual information as to the rates to be charged. I should repeat that I am not concerning myself with bricks by the thousand, but with bricks by the ton, leaving the operator to work out for himself the rate per thousand, according to the weight of the bricks. If those bricks weigh, for example, 2f tons per thousand, then to arrive at a rate per thousand, he must multiply the rate per ton given in this article by 2f, and so on, I propose to follow the procedure of the previous article and deal first with a 10-mile lead. The terminal times and charges are set out in Table III, so that there is no need to go into those in each example. It is the travelling times with which I am immediately concerned,
Costs for 10-Mile Lead
It has already been established that for a three-mile lead the time is 361 minutes. For a 10-mile lead there are seven more miles to be run in each direction at 3 minutes per mile, requiring 42 minutes. The total travelling time, out and home, for a 10-mile lead will, therefore, be 781 minutes.
Now, for the 7-8-tonner we must charge at the rate of 12s. per hr. and the cost of 781 minutes at that price is 15s. 9d. To that sum must be added 7s. 1 ld.-the rate for 20 miles at 4Id. per mile, The final rate is thus made up of 15s. 9d. for travelling time, 33s. for terminal delays (see Table III) and 7s. lid, for mileage. The total is £2 16s. 8d„ and for a 71-ton load that works out at 7s. 6d. per ton.
In the case of a one-mile lead, the travelling time will be 20 minutes, and that, at 12s. per hr., equals 4s. Add for two miles at 41c1.. which is 91d., and again 33s. for the terminal delays and we get a total of 37s 91d., which, for a 71-ton load, equals 4s. 10d. per ton.
For a two-mile lead the time is 30 minutes, costing 6s.; there are four miles run at 4id. per mile (Is 7d.) and
terminal delays account for 33s., so that the total is 40s. 7d. 5-d. per ton.
Proceeding in the same way to deal with the three-mile lead, the travelling time is 36f minutes, which costs 7s. 4d.; six miles at 41d. per mile cost 2s. 2fd. and the total, including 33s. for terminal delays, is 42s. 6fd., or 5s. 8d. per ton.
Each additional mile beyond the three miles takes 6 minutes to travel (one mile each way) and costs Is. 2fd., in addition to which there is 91d. for mileage, giving the total of 2s. Therefore, rather more than 3d. per mile must be added for each additional mile lead.
It should not be necessary to deal in such detail as above with the other two sizes of vehicle. The method is precisely the same; only the figures are different, being as set down in Table III. I have worked them out carefully and they are incorporated in Table IV, which also includes the figures quoted in the previous article for the first three types of vehicle. • As might be expected, the largest vehicles, carrying the biggest tonnage, can haul the load at a much lower rate than the smaller ones, but one or two results which may surprise some readers are to be observed.
Petrol. and Oil Costs Compared An operator with a 6-ton oiler should charge Id. or 2d. more per too for leads up to three miles, but beyond that mileage the rate is less than for either the 6-ton petrol lorry or, of course, the 5-tonner. Thereafter the rate gradually diminishes as the mileage increases, until at 150 miles it is actually is. 10d. per ton less.
The 7-8-tonner is the most expensive for the first 12 miles, after which the rate begins to compare favourably with that of the 5-tonner, but is practically the same as for the 6-ton petrol-engined vehicle and actually more than for the 6-ton oiler. This is the most important point to note, and the difference—the comparatively greater cost and, therefore, the higher rate to be charged—arises entirely from the assumption that the larger vehicle does not exceed the maximum legal speed of 20 m.p.h.
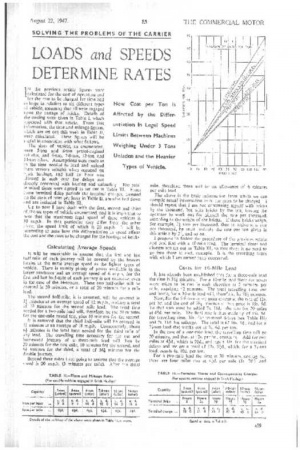
The position as regards these rates and the respective vehicles is, perhaps, more clearly shown in Fig. 1, which contains curves of the rates to be charged for the different vehicles. It will be noted that there are only five curves, whereas I am dealing with six vehicles. The reason is that, as there is so little difference in the charge to be made f r the 6-ton •petrol vehicle and the 7-8-ton oiler, one curve serves the two vehicles.
The original point I had in view when preparing this article was to demonstrate the difficulty of agreeing a flat rate per ton for traffic without taking into consideration the size of vehicle which is to be used. In this case, for example, taking the 50-mile lead, it would seem that, using a 6-ton petrol vehicle, 17s. 6d. per ton would be a fair rate. On that basis, the operator using a 5-tonner would not be able to compete, as he would be 2s. per ton short of the minimum rate required to raise a reasonable profit. On the other hand, the operator of a 12-tonner or 14-tonner would be satisfied with a rate 3s. per ton less than that which is necessary in the case of the 6-ton petrol-engined vehicle.
Another point which arises is, perhaps, best illustrated by comparing the figures for the 6-ton petrol vehicle and the 6-ton oiler. There is a difference in favour of the oiler which amounts, over the maximum lead quoted, to Is. 10d. per ton, and even at 50 miles the discrepancy is Is. per ton. The question which is often asked is, how should the rate be assessed; should it be based on the figures for an oilengined vehicle, or on those for a petrol-engined vehicle?
The answer is something which cannot be calculated at all. If the user of the oiler can obtain the rate which will show a profit upon a petrol-engined vehicle, he will reap the benefit of his forethought in purchasing a vehicle that is less expensive to run. On the other hand, if the state of the market be such that the maximum rate to be obtained be that which is reasonably profitable with an oil-engined vehicle, and only barely profitable with a petrol-engined machine, then, again, the owner of the oiler reaps the benefit of his enterprise.
Taking the long view, it seems that if oil-engined vehicles be suitable for the work and be obtainable, a fair thing is to assess the rate on the basis of the most efficient type of vehicle, which will mean that, in the long run, owners of petrol-engined vehicles will be compelled by force. of circumstances and economics to buy the more efficient machine, S.T.R.
















































































