Worm Contact.*
Page 16
If you've noticed an error in this article please click here to report it so we can fix it.
Though the subject of worm-gearing has been less thoroughly explored than that of spur-gearing, it might nevertheless be anticipated that little remains to be said on either from a purely theoretical point of view. Experimental investigation of the actions involved in worm-gearing has been singularly incomplete, but many writers have contributed to the theory of the subject. In spite of what has been written, some of the most interesting aspects of the question have been overlooked or ignored, with the result that there is no single source from which a complete account of the action of worm-gearing can be gathered. The present paper is intended rather to cover some of the more obvious omissions than to give a complete account of this form of gearing. A complete explanation would be impossible within the compass of a paper of reasonable length. The comparative completeness of the theory of spur-gearing is due to the fact that the whole action of such gears may he studied in a single plane perpendicular to the axes about which motion takes place. The successive positions of the toothprofiles in this plane, though not capable of continuous representation on a plane diagram, may be drawn at close intervals, and a tolerably clear conception of the motion may begathered by the aid of a corresponding series of figures.
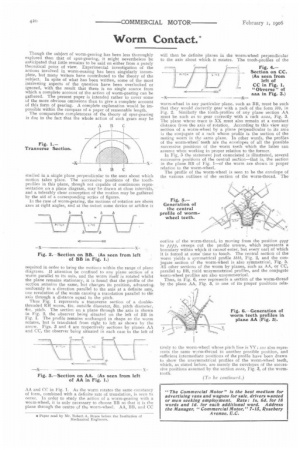
in the case of worm-gearing, the motions of rotation are about axes at right angles, and at the outset some device or artifice is required in order to bring the motions within the range of plane diagrams. If attention be confined to any plane section of a worm parallel to its axis, and the worm itself is rotated whilst the plane remains stationary, it is found that the profile of the section remains the same, but changes its position, advancing uniformly in a direction parallel to the axis at a definite rate, one revolution of the worm causing a translation parallel to the axis through a distance equal to the pitch, Thus Fig. 1 represents a transverse section of a doublethreaded RH worm, 4in. outside diameter, 3in. pitch diameter, 4in. pitch. The section on a plane through the axis is shown in Fig. 2, the observer being situated on the left of BB in Fig. I. The profile remains unchanged in shape as the worm rotates, but is translated from right to left as shown by the arrow. Figs. 3 and 4 are respectively sections by planes AA and CC, the observer being situated in each case to the left of
AA and CC in Fig. 1. As the worm rotates the same constancy of form, combined with a definite rate of translation, is seen to occur. In order to study the action of a worm-gearing with a worm-wheel, it is only necessary to choose BB so that it is the plane through the centre of the worm-wheel. AA, BB, and CC will then be definite planes in the worm-wheel perpendicular to the axis about which it rotates. The tooth-profiles of the
worm-wheel in any particular plane, such as DB, must be such that they would correctly gear with a rack of the form bbb, Fig. 2. Similarly the tooth-profiles of any plane section AA must be such as to gear correctly with a rack aaaa, Fig. 3. The plane whose trace is XX must also remain at a constant distance from the axis of rotation. According to this view any section of a worm-wheel by a plane perpendicular to its axis is the conjugate of a rack whose profile is the section of the mating worm in thsi same plane. Iu other words, the profiles of the worm-wheel teeth are the envelopes of all the possible successive positions of the worm teeth which the latter can assume when working in proper relation to the former.
In Fig, 5 the statement just enunciated is illustrated, several successive positions of the central section—that is, the section in the plane BB of Fig. 1—of the worm are shown in proper relation to the worm-wheel.
The profile of the worm-wheel is seen to be the envelope of the various outlines of the section of the worm-thread. The outline of the worm-thread, in moving from the position gm to Attp, sweeps out the profile evenew, which represents a boundary within which it cannoe enter, but every oart of which it is forced at some time to touch. The central section of the worm yields a symmetrical profile bbbb, Fig. 2, and the conjugate section of the worm-wheel is also symmetrical, Fig. 5. All other sections of the worm by planes, such as AA, or CC, parallel to BB, yield unsymmetrical profiles, and the conjugate worm-wheel profiles are also unsymmetrical. Thus, in Fig. 6, erre represents a section of the worm-thread by the plane. AA., Fig. 3, in one of its proper positions rela tively to the worm-wheel whose pitch line is 'VII; MS also represents the same werm-thread in another possible position, and sufficient intermediate positions of the profile have been drawn to show the unsymmetrical profiles of the worm-wheel teeth, which, as stated before, are merely the envelopes of the successive positions assumed by the section aezaa, Fig. 3, of the wormtooth.




















