RAISE SPEED AND US]
Page 46
Page 47
If you've noticed an error in this article please click here to report it so we can fix it.
ROADS TO CAPACITY
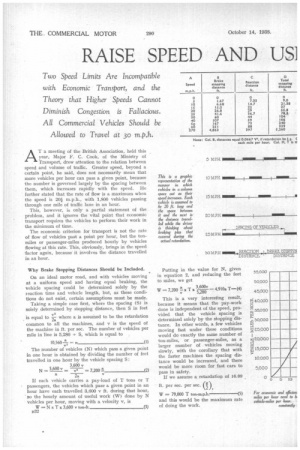
AT a meeting of the British Association, held this year, Major F. C. Cook, of the Ministry of Transport, drew attention to the relation between speed and volume of traffic. Greater speed, beyond a certain point, he said, does not necessarily mean that more vehicles per hour can pass a given point, because the number is governed largely by the spacing between them, which increases rapidly with the speed. He further stated that the rate of flow is a maximum when the speed is 201. m.p.h., with 1,800 vehicles passing through one mile of traffic lane in an hour.
This, however, is only a .partial statement of the problem, and it ignores the vital point that economic transport requires the vehicles to perform their work in the minimum of time.
The economic criterion for transport is not the rate of flow of vehicles past a point per hour, but the tonmiles or passenger-miles produced hourly by vehicles flowing at this rate. This, obviously, brings in the speed factor again, because it involves the distance travelled in an hour.
Why Brake Stopping Distances Should be Included.
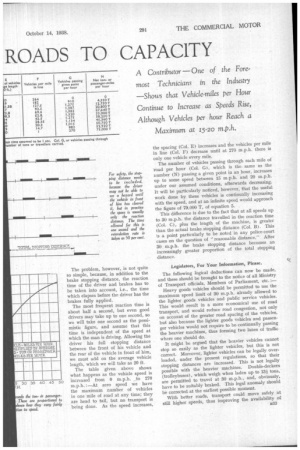
On an ideal motor road, and with vehicles moving at a uniform speed and having equal braking, the vehicle spacing could be determined solely by the teaction time and vehicle length, but, as these conditions do not exist, certain assumptions must be made.
Taking a simple case first, where the spacing (S) is solely determined by stopping distance, then S in feet
is equal to Nk. where a is assumed to be the retardation
common to all the machines, and v is the speed of the machine in ft. per sec. The number of vehicles per mile in line is 5,280 S, which is equal to • 0,560n— --(1)
v2
The number of vehicles (N) which pass a given point in one hour is obtained by dividing the number of feet travelled in one hour by the vehicle spacing S: 3,600 v
N = 3'600 v v2 = 7,200 a (2) 2a
If each vehicle carries a pay-load of T tons or T passengers, the vehicles which pass a given point in an hour have each travelled 3,600 v ft. during that hour, so the hourly amount of useful work (W) done by N vehicles per hour, moving with a velocity v, is W =N x Tx 3.600 v ton-ft.
B32
The problem, however, is not quite SO simple, because, in addition to the brake stopping distance, the reaction time of the driver and brakes has to be taken into account, i.e., the time which elapses before the driver has the brakes fully applied.
The most frequent reaction time is about half a second, but even good drivers may take up to one second, so we will take one second as the pessimistic figure, and assume that this time is independent of the speed at which the man is driving. Allowing the driver his full stopping distance between the front of his vehicle and the rear of the vehicle in front of him, we must add on the average vehicle length, which we will take as 20 ft.
The table given above shows what happens as the vehicle speed is increased from 0 m.p.h. _ to 270 m.p.h. :—At zero speed we have the maximum number of vehicles in one mile of road at any time; they are head to tail, but no transport is being done. As the speed increases,
the spacing (Col. E) increases and the vehicles per mile in line (Col. F) decrease until at 270 m.p.h. there is only one vehicle every mile.
The number of vehicles passing through each mile of 'road per hour (Col. G), which is the same as the number (N) passing a given point in an hour, increases up to some speed between 15 m.p.h. and 20 m.p.h. under our assumed conditions, afterwards decreasing. It will be particularly noticed, however, that the useful work done by these vehicles is continually increasing with the speed, and at an infinite speed would approach the figure of 79,000 T, of equation 5.
This difference is due to the fact that at all speeds up to 30 m.p.h. the distance travelled in the reaction time (Col. C), plus the length of the machine, is greater than the actual brake stopping distance (Col. B). This is a point particularly to be noted in any police-court cases on the question of "reasonable distance." After 30 m.p.h. the brake stopping distance becomes an increasingly greater proportion of the total stopping distance.
Legislators, For Your Information, Please.
The following logical deductions can now be made, and these should be brought to the notice of all Ministry of Transport officials, Members of Parliament, etc. :—
Heavy goods vehicles should be permitted to use the maximum speed limit of 30 m.p.h. already allowed to the lighter goods vehicles and public service vehicles. This would result in a more economical use of road transport, and would reduce road congestion, not only on account of the greater road spacing of the vehicles, but also because the lighter goods vehicles and passenger vehicles would not require to be continually passing the heavier machines, thus forming two lanes a traffic where one should do.
It might be argued that the heavier vehicles cannot stop so easily as the lighter vehicles, but this is not correct. Moreover, lighter vehicles can be legally overloaded, under the present regulations, so that their stopping distances are increased. This is not legally possible with the heavier machines. Double-deckers (trolleybuses), which weigh when laden up to 13i tons, are permitted to travel at 30 m.p.h., and, obviously, have to be suitably braked. This legal anomaly should be corrected at the earliest possible moment.
With better roads, transport could move safely, at still higher speeds, thus improving the availability of B33




























































































