Ball Bearings An Analysis.
Page 3

Page 4
Page 5

If you've noticed an error in this article please click here to report it so we can fix it.
By Herbert Guthrie.
A complete study of ball bearings is one of those matters which calls for a lot of experience, and a high ability to analyse the theoretical points involved in the different kinds of bearings. The subject, in spite of accumulated evidence from machinery owners who have applied them, is extremely difficult : it is well-nigh impossible to make any positive deductions of importance, and that, to a large extent, because the personal equation, or prejudice, is involved. Prolonged comparative experiment, under the direction of an unbiassed mind, is required : this, the writer submits, we, unfortunately, have not yet enjoyed. He has put in a number of ball bearings, the numerous sets varying largely in size and circumstance ; he has constructed them on certain unusual principles, and has never had reason to regret their designs, though those principles, as carried out by some well-known firms, have been declared by them to be impracticable. The only thorough investigation the writer has heard df■ on this subject was made by a German scientist, Professor Stribeck, who has been kind enough to supply a copy of his report, and his treatise, it must at once be confessed, does not back up the deductions indicated in this article. The report, however, clearly favours the type shown in Fig. 4, as the best for heavy bearings, and Type 6 is stated to have double the amount of friction, each taken at maximum load and speed. This the writer cannot conceive to be correct, as it is a result so different from the theoretical deductions herein. Practical men often say : " Oh, yes ; your theories are all very well, but a pennyworth of practice is worth a pound's worth of theory." My answer to that is, these socalled practical men are often the worst enemies to progress They forget that true theory is the best practice. If practice does not back up a certain theory, then something is missing in the problem, though we cannot say where until the reasons for the difference are discovered. In such very delicate experiments as these, a minute difference in any part of the apparatus would vitiate the figures considerably ; but, admitting a greater amount of friction in Type 6, friction, after all, is not the only consideration. If we do get a little more friction, and there is a much longer life, coupled with a cheaper construction, then Type 6 is decidedly the better for road locomotion and ordinary purposes. Type 6, with double the working area of bearing, will, obviously, have a longer life than Type 4.
It will be universally acknowledged that the actual crushing strength of the balls is so great, as compared with the load they are usually called upon to bear, that breakage of the balls is not worth further consideration. Ball bearings do not give out from collapse of the balls, but from the wear of the surfaces of both the balls and the races. One of the first objects to be secured, then, is a large working surface, and this under all conditions..
Let us summarise the different types :— Fig. i indicates the simplest of all, a single-track ball running between two flat surfaces. Its axis is a, and the track on which it runs is the thick equatorial line.
Fig. 2 is the case of running between three flat surfaces, the bottom two forming one V-shaped race There are three tracks on this ball, indicated by the three thick lines.
Fig. 3 is the cast. of four flat surfaces, forming two Vshaped grooves, and two tracks on the balls. Figs. 4, 5, and 6 are a similar variety of types, but with curved race surfaces in order to broaden the effective working surfaces, and, therefore, to procure longer life. The usual race radius is from two-thirds to three-quarters the diameter of the ball.
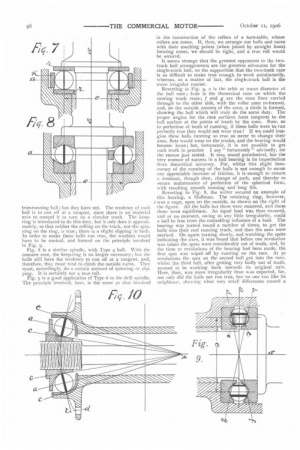
In the practical application, we will start with the most primitive of all cases under Type 1, the bearing to carry a vertical shaft, or that bearing which is often used for a drilling-machine spindle, as represented by Fig. 7. The principle involved here is that of the turn-table running on disc wheels : s is the vertical shaft, rr the races, formed of hard steel washers, and h the keep-ring to prevent the balls from flying out. Now, it is commonly argued that each ball runs on its equator (indicated by the thick line), and spins on its axis (a), the keep-ring revolving at half the pace of the spindle, and the designers think they have a true-running ball ; but they have not. The tendency of each ball is to run off at a tangent, since there is no material axis to compel it to turn on a circular track. The keepring is introduced to do this duty, but it only does it approximately, so that neither the rolling on the track, nor the spinning on the ring, is true ; there is a slight slipping in both. In order to make these balls run true, the washers would have to be conical, and formed on the principle involved in Fig. 9.
Fig. 8 is a similar spindle, with Type 4 ball. With the concave race, the keep-ring is no longer necessary; but the balls still have the tendency to run off at a tangent, and, therefore, they must tend to climb the outside curve. They must, accordingly, do a certain amount of spinning or slipping. It is certainly not a true roll. Fig. g is a good application of Type 6 to the drill spindle. The principle involved, here, is the same as that involved in the construction of the rollers of a turn-table, whose rollers are cones. If, then, we arrange our balls and races with their touching points (when joined by straight lines} forming cones, we should be right, and a true roll would be secured.
It seems strange that the greatest opponents to the twotrack ball arrangements are the greatest advocates for the single-track ball, on the supposition that the two-track race is so difficult to make true enough to work satisfactorily, whereas, as a matter of fact, the single-track ball is the more irregular runner.
Reverting to Fig. 9, o is the orbit or mean diameter of the ball race; bcde is the theoretical cone on which the moving track rests; f and g are the cone lines carried through to the other side, with the roller come re-formed, and, on the outside corners of the cone, a circle is formed,. showing the ball which will truly do the same duty. The proper angles for the race surfaces form tangents to the ball surface at the points of touch by the cone. Now, as to perfection of truth of running, if these balls were to run perfectly true they would not wear true ! If we, could imagine these balls running so true as never to change their axes, flats would wear on the tracks, and the bearing would become loose; but, fortunately, it is not possible to get such truth in practice I say " fortunately " advisedly, for the reason just stated. It may sound paradoxical, but the very essence of success in a ball bearing is its imperfection from theoretical accuracy. For, whilst this slight inaccuracy of the running of the balls is not enough to cause any appreciable increase of friction, it is enough to ensure a constant, though slow, change of path, and thereby to. secure maintenance of perfection of the spherical form,. with resulting smooth running and long life.
Reverting to Fig. 8, the writer secured an example of this bearing, a Hoffman. The retaining ring, however, Iva§ a cage, open on the outside, as shown on the right of the figure. All the balls but three were removed, and these three were equidistant. An equal load was thus ensured, and at no moment, owing to any little irregularity, could a ball be free from the controlling influence of a load. The bearing was turned round a number of times, to get the balls into their real running track, and then the axes were marked. On again turning slowly, and watching the spots indicating the axes, it was found that before one revolution was taken the spots were considerably out of truth, and, by the time 21 revolutions of the bearing had been made, the first spot was wiped off by running on the race. At 30 revolutions the spot on the second ball got into the race, whilst the third ball, after getting very badly out of truth, seemed to be working back towards its original axis. Here, then, was more irregularity than was expected, for, not only did the balls not run true, but no one ran like its neighbour, showing what very small differences caused a
change of track. I could find no fault with the bearing. It was made as perfect as any such bearing can be made; in fact, the name of Hoffman is a sufficient guarantee.
It would be difficult to find a better illustration of good, practical results, from irregular-running balls, than that of the standard type of bicycle bearing, as shown by Fig. TO. In this case, let us suppose we have a turn-table to be carried on disc wheels, since it is a single-track design, and, further, since adjustment has to be made at approximately right angles to the pressure, inclined races are essential. Point p on the spindle axis is chosen as yielding a convenient generating centre and angle of track, In erder to give the maximum range of adjustment. Radius lines (aa) are supposed to be the axes on which the balls turn, whilst cc are the angles of the races upon which they run at the points where the arc (d) intersects them. Of course, balls running between inclined planes will tend to run out towards the mouth, and, no doubt, do so in this case until they find parallel touch points, so that these would be not on the arc (d) but on the tangent line (I). Under these circumstances, then, there is no hope of a ball's running true on the original axis (a) ; but, what is "running true "? Balls are capable of a genuine roll, other than in straight lines I A ball will roll in a circle on a table, though it is a compound motion. The ball has to be constantly rolling inwards, as well as onwards, in order to follow the curve and to avoid following a tangent ; but, when squeezed between two surfaces, a ball is not free to roll inwards. There seems to be nothing for it, then, except climbing the track outwards until it gets far enough to roll in a V, and to admit of a certain amount of spinning
• in its orbit : and it is this continuous change of track that maintains the spherical form, and good working conditions, so much sought for by users.
One would think that this bearing, as applied to the barrel hub, would not be so good, since the track on the balls is not so directly in line with the load to be resisted, the cup and cone being reversed. The practical inferiority, none the less, is so microscopic as to be inappreciable. This
EMTORIAL communications must be addressed to The Editor," and should reach the London Office not later than 1st post on Monday, if intended for the following Thursday's issue. The Editor does not hold himself responsible for the safe keeping or return of anything submitted
For his consideration ; but if stamps are enclosed, MSS., drawings or photographs which are not considered suitable will be returned.
All articles, drawings, photographs, and other contributions paid for and published in this journal are the copyright of the proprietors of "The Commercial Motor," from whom alone authority to republish can he All letters regarding advertisements. subscriptions. and other business matters must be addressed to "The Manager," The circulation of "The Commercial Motor" is certified monthly by a firm of Chartered Accountants.
For further information regarding Subscriptions,Advertieements, Deposit System, etc., see " Notices," Column 1 of Sundry Advertisements. (kl
kind of bearing is what we might justly call a " doublepurpose bearing," for it resists side thrusts at the same time that it carries weight. It is not, however, a kind used for heavy work, and, as far as the writer can find out to-day, the tendency is in the direction of single-track balls, so that double-purpose bearings have to be furnished with separate rings of balls to fulfil each purpose.






















